近日，山西大学理论物理研究所李卫东教授课题组与法国巴黎高等师范学院M. Gessner博士以及意大利学者A. Smerzi 研究员合作，在多体量子纠缠结构分析上取得了重要的进展。该成果提出了一对实验可检测的、对测量精度依赖的物理量，并由此实现量子多体纠缠结构分析的新方法；该研究结果对深入理解多体量子纠缠、特别是多体量子结构具有重要的理论意义；对推动其在量子精密测量中的进一步应用具有重大意义。文章以“Metrological Detection of Multipartite Entanglement from Young Diagrams”为题于2021年2月25日发表在《物理评论快报》[Phys. Rev. Lett. 126, 080502 (2021)]，该文第一作者为在读博士研究生任志红。

在多体量子系统中，量子纠缠态的有效分类对于深入理解量子纠缠本身以及量子信息科学的发展都具有非常重要的意义。当前，人们广泛使用的描述多体量子关联的方法可以总结为两种方式：“纠缠深度(entanglement depth)”和“k-可分性(k-separability)”。最近，S. Szalay注意到多粒子量子纠缠态具有粒子交换对称不变性，从而将量子多体纠缠结构与整数分拆的基本数学概念建立了一一对应的联系。利用杨图表示方法，纠缠深度和可分割部分的数目分别与杨图的宽度和高度相对应，而杨图的宽度和高度之差，即戴森秩(Dyson’s rank)，可用以描述态的可延性(stretchability) [Quantum 3, 204 (2019)]。这些分析从根本上提供了理解量子多体纠缠可行的数学方法。但是，如何将这些数学方法用实验可观测量进行表示，将对多体量子态的纠缠结构的判断和应用具有重要意义。

在这个工作中，提出并分别证明量子费舍信息(Quantum Fisher information)和自旋压缩系数(spin-squeezing coefficients)可用于对多体系统的纠缠结构进行有效的分析。文章不仅从数学上证明了其可行性，而且成功用于若干已发表的实验结果的分析。图1和图2展示了其中两个例子。结果表明：采用单参数判据时，戴森秩多数情况下比用纠缠深度和k-可分性要好，尤其是纠缠深度远小于总粒子数时。其次，对于多体系统的纠缠结构分析，使用联合杨图的宽度和高度构造的判据比单独使用上述三个参数之一发展的判据更为有效。

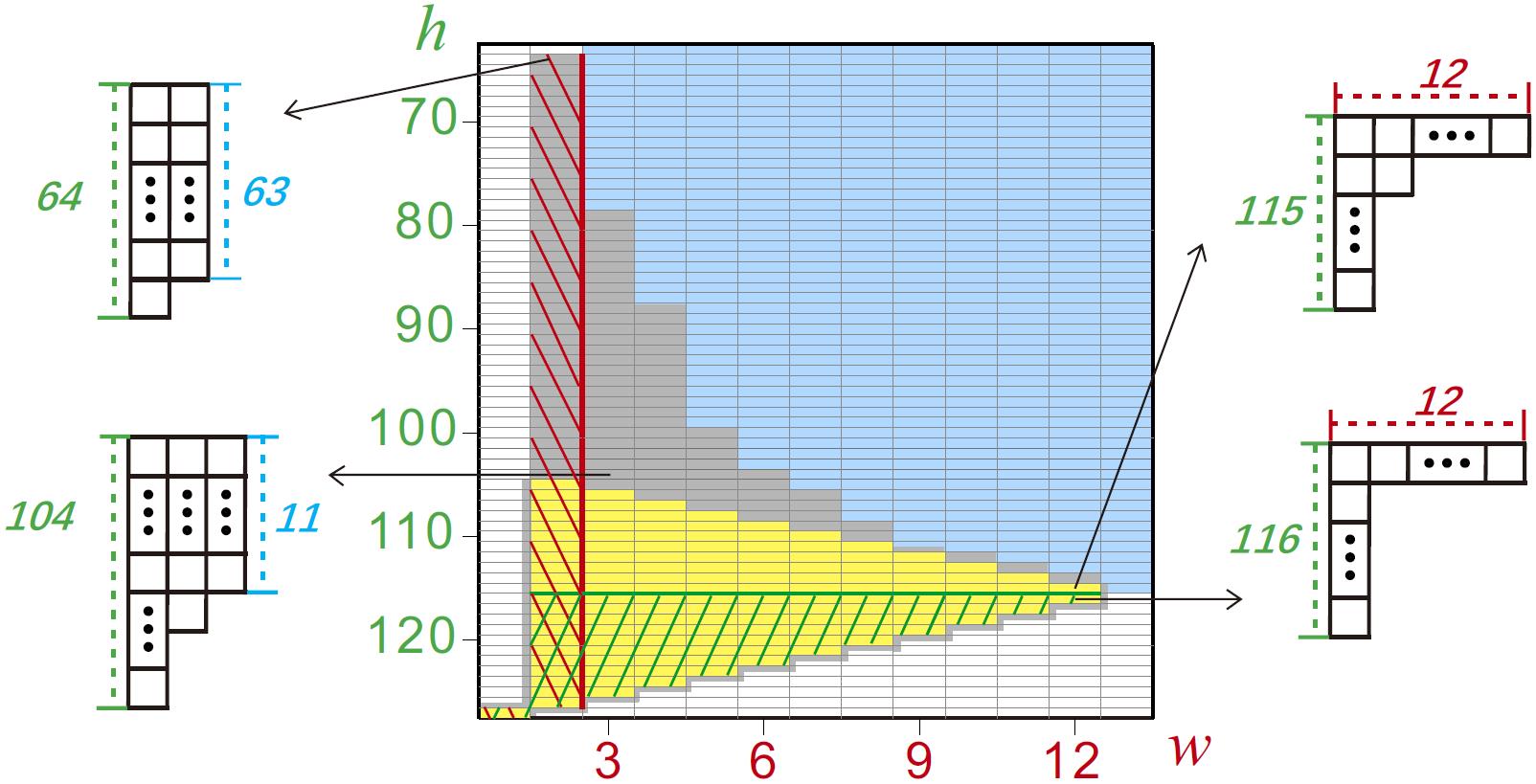
图1 N=127的量子多体GHZ态[Science 352, 1297 (2016)]的纠缠结构分析，其中所测的量子费舍信息值F_Q≥266.7。

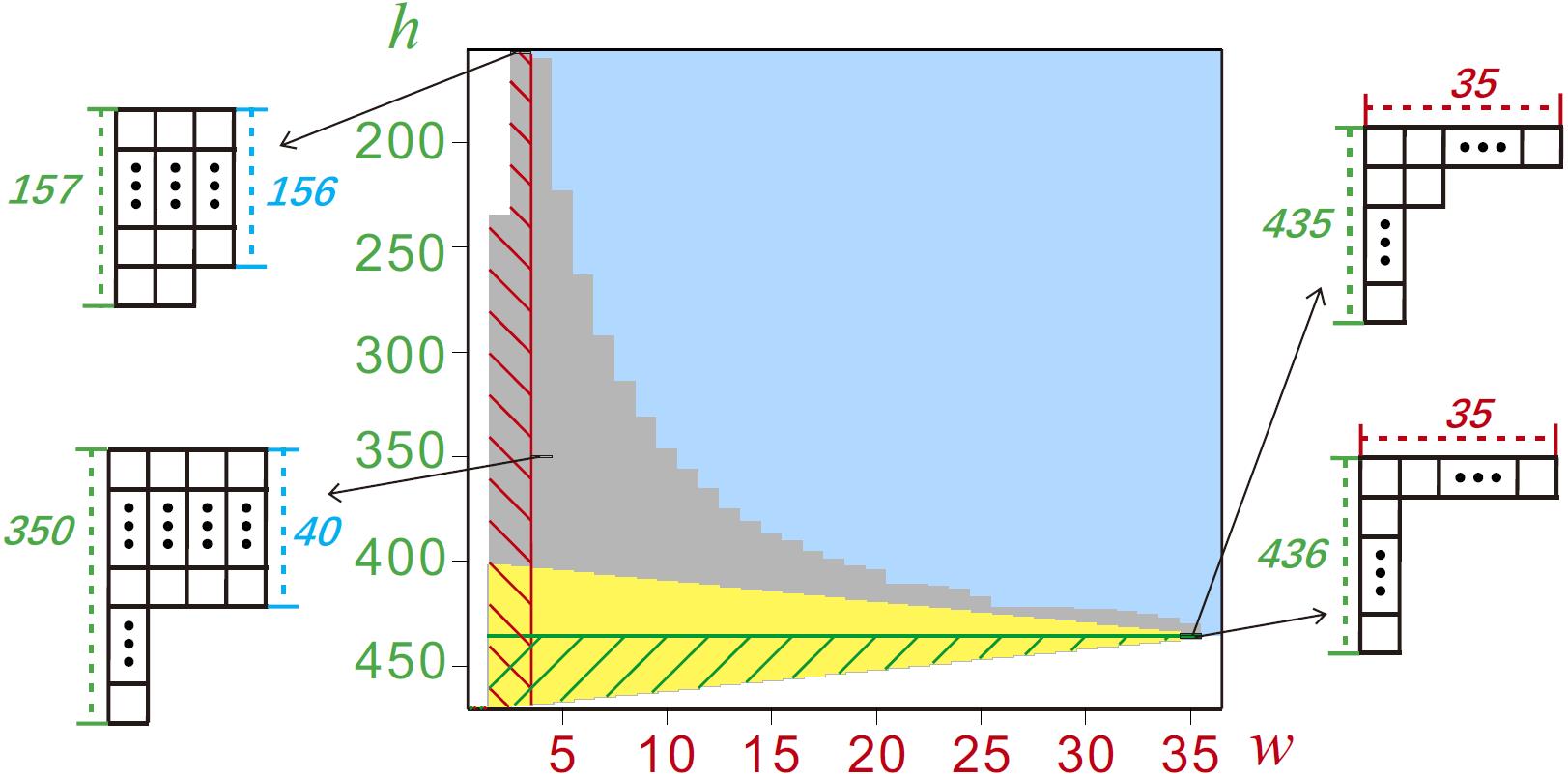
图2 N=470的量子多体GHZ态[Science 345, 424 (2014)]的纠缠结构分析，其中所测的自旋压缩系数ξ²≤-4.5dB。

该项研究受到国家重点研发计划，国家自然科学基金，111计划，山西省人才计划和法国巴黎高等师范学院实验项目(LabEx ENS-ICFP: ANR-10-LABX-0010/ANR-10-IDEX-0001-02 PSL)资助。

论文链接：https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.080502